Welcome to the Raspberry Pi Passphrase Generator

quietly uganda expo moulds warheads congestion aidesdecamp

with 244 bits of entropy

If an attacker knows your method of choosing a passphrase, your Entropy will be about 111 bits. Each word is worth about 15.82 bits of entropy (because 2^15.82 is about 57,850). So with seven words you have a passphrase with about 111 bits of entropy (15.82 x 7 = ~111). This would still take up to 500 billion years (average 250 billion years) to crack at 100,000,000,000,000 (100 trillion) guesses per second. Replacing a few characters with upper case and special characters will dramatically improve the entropy even when an attacker knows what method you used.

Dictionary of 58109 words taken from

http://www.mieliestronk.com/corncob_lowercase.txt

Inspired by Micah Lee's Diceware Passphrases

https://firstlook.org/theintercept/2015/03/26/passphrases-can-memorize-attackers-cant-guess/

An awesome image of time needed to crack based on entropy, passphrase length and brute-force attacks per second

Our entropy is measured as log2(26^passlength) assuming the attacker does not know the method you used to generate your passphrase, otherwise the entropy is 111 bits

=================================================================

Update 8 20171126

Just a quick update to avoid the slight risk of running out of random bytes.

I had initially taken 40 random bytes in one go, and used 2 for each word, but there is a slight risk of getting 14 above 58109

So now I just get them 2 bytes at a time in the function to get a word as so:

$id=floor(hexdec(bin2hex(openssl_random_pseudo_bytes(2))));

while ($id>58109 || $id<1) // possible values 0-65535

{

$id=floor(hexdec(bin2hex(openssl_random_pseudo_bytes(2))));

}

=================================================================

Update 7 20161018

I decided a while back to allow ECC using the NIST's top secret allowed curve (ECDH secp384r1) which is supported by recent versions of Firefox making it lightning fast (as well as the strong RSA & DH params they also mandate rather than any other elliptic curve).

I'm still waiting for chacha20 stream cypher support on Raspbian though.

The RPi was offline for a while during a move so we lost Tor HSTS preloading but it's still available for Chrome, Edge, Firefox and IE

Interestingly, I'm still getting a huge amount of DHE rather than ECDHE traffic, which tends to go against the perceived wisdom of the Lets Encrypt community that DHE only tends to be used with insecure settings ( we have DHE-RSA-AES256-SHA probably for older versions of Firefox and DHE-RSA-AES256-GCM-SHA384, which together are more prevalent than ECDHE-RSA-AES256-GCM-SHA384 and are no less weaker). We're still A+ with 100% in all categories for SSLLabs, naturally!

=================================================================

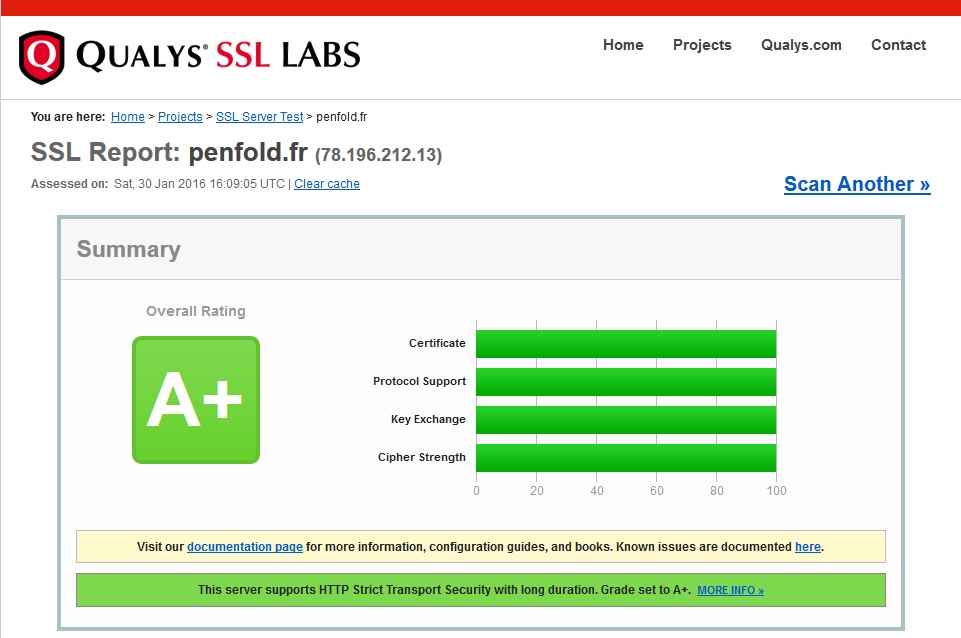
Update 6 20160130

I've upgraded to a 4096 bit RSA SSL key and 4096 bit DH parameters for Ephemeral Key Exchange (I'm using my own DH parameters rather than the ones provided by default) and have removed all Elliptic Curve algorithms. This is going to hammer the poor old Pi but the NSA is recommending Government use longer-key RSA and DHE instead of ECC. But their rationale stinks rather:

Q: The commercial world appears to be moving to elliptic curves. Why is NSA continuing to support older algorithms?

A: NSA supports the use of NIST P-384 in NSS. In the original CNSSP-15 both RSA and Diffie-Hellman were included as legacy algorithms which were only to be used until replacement elliptic curve cryptography (ECC) equipment was available. Since that time NSA has come to appreciate that some of these legacy systems will be around for much longer than we had planned. Because of these legacy systems and because there is an eventual need to move to quantum resistant public key algorithms, NSA has decided that it may be more cost effective for some NSS to continue to use RSA and Diffie-Hellman with larger key sizes until the new quantum resistant public key algorithms are ready.

Here is a copy of the NSA report

=================================================================

Update 5 20151130

The site has been accepted on the Chrome HSTS preload list and has been propagated to Edge, Firefox and IE. Only Tor has yet to be updated to preload the penfold.fr URL.

=================================================================

Update 4 20151104

Yay! The little Pi now has a letsencrypt TLS key with an "A+" rating from https://www.ssllabs.com/ so we're pretty secure in communicating the passphrase. Thanks to the Lets Encrypt people for the certificate and Ivan Ristic for SSL/TLS tips. I've also added HSTS and am waiting for the Chrome HSTS preload list to accept my site to further mitigate risk of your passphrase being intercepted.

=================================================================

Update 3 20151027

I've got it running on a Raspberry Pi at home but am still waiting to get a letsencrypt TLS key using a decent TLS setup for secure passphrase communications. For now you can use my self-signed key if you want https://penfold.fr

=================================================================

Update 2 20150801

I'm using an internal array rather than an external database, to avoid having the passphrase words go over the internet in cleartext (the db was hosted separately). Next step is to put it on a Raspberry Pi at home and get a letsencrypt TLS key using a decent TLS setup for secure passphrase communications.

=================================================================

Update 1 20150413

I've replaced the PHP rand() function with openssl_random_pseudo_bytes(40), giving 20 x 65536 variability using one call, retrying for each word until the 64k number is at or below 58109. The problem with rand() is that it's not as unpredictable as we'd like. Whereas openssl_random_pseudo_bytes() uses /dev/urandom and is "computationally secure" enough. Here is why urandom is more than good enough

=================================================================

I've hastily implemented this ~~using PHP rand() and I have no idea how that affects entropy, but as~~ my source list is 58000 words rather than the 7776 in Diceware there should be a one in, ooh, several gazillion chance of guessing it on average. See Micah Lee's article for real details on how that kind of thing works.

Each word from the list is worth about 15.82 bits of entropy (because 2^15.82 is about 57,850). So if you choose seven words you’ll end up with a passphrase with about 111 bits of entropy (because 15.82 x 7 = ~111) ~~assuming the PHP rand() function on the hosted OS is anywhere near optimal~~.

Note: I'm not a web developer and have just hacked this together using a PHP template, so be gentle with me... I just thought this would be fun. Any constructive comments would be welcome on my Twitter account @PenfoldDavid . I don't allow you to enter your own numbers à la Diceware as I'd have to deal with all the smart alecs trying to fuzz it.

If you're not accessing this via a secure connection (mainly because I haven't set it up properly yet) you're better off using Diceware, randomly sticking your finger into a dictionary or banging your keyboard with your head.

Also, the database is hosted separately so the words are going over the internet in clear text. It's probably not wise to use this to encrypt a disk if you're a Five Eyes target. I'll rebuild it some time in a different language so that it can take a local array of all words rather than selecting the specific words from the DB.

I'll probably restrict the words to 10 letters or less too, as some of these are pretty hard to remember.

This has been fun, but you're probably best using a "hair-gapped" method of generating your passphrase, i.e. the generation of your passphrase stays in your noggin rather than coming from a computer